
The Solver is an add-in embedded in Microsoft Excel. The most challenging part of nonlinear regression is determining the parameter (θ) theta 1, theta 2, etc., starting points. A scatterplot of the data can be constructed and a plausible nonlinear model determined by juxtaposing the scatterplot with graphs of nonlinear models. Combining a mechanistic model with an empirical model provides the best of both worlds. Small pilot runs can be used for data gathering if no data exists. Mechanistic models are constructed purely from physical considerations, whereas empirical models are built from data. In these cases, combining a mechanistic model with an empirical model is a practical approach.
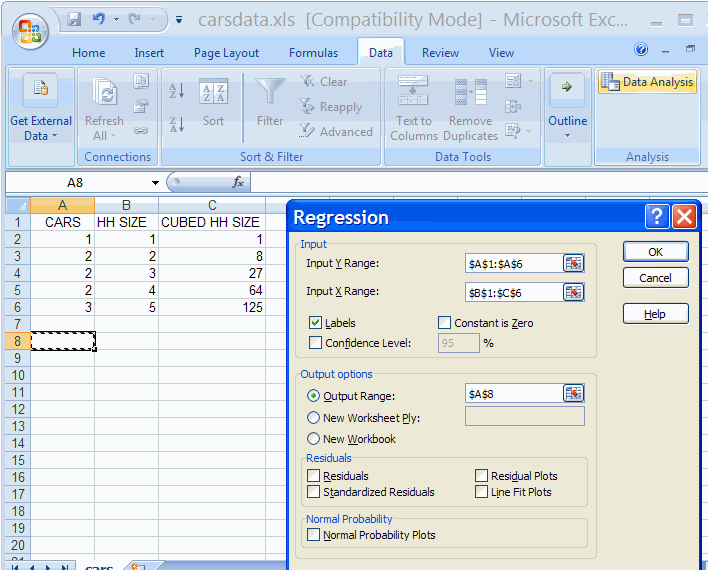
Without this knowledge, it is challenging to choose a nonlinear model and its starting parameters. Researchers may not know the actual model tendency of the dependent variable (Y) and the independent variable (X). Selecting the model and parameter (θ) starting points (theta 1, theta 2, etc.) requires effort on the researcher's part. When constructing a nonlinear regression model, the model itself must be chosen along with the parameter (θ) starting points (theta 1, theta 2, etc.). The predictor variable (X) may or may not appear in the first-order.
The regression equation has parameters (θ) theta 1, theta 2, etc., that may be expressed as exponents, multiplied or divided by another parameter, etc. Nonlinear regression models are not first-order models. Nonlinear regression is a different animal. Simple linear regression is a good starting point for exploring statistical relationships. The predictor variable (X) appears only in the first-order. The regression equation has no parameters (β0 intercept or β1 slope) expressed as an exponent, nor are they multiplied or divided by another parameter. Simple linear regression models are considered first-order models. Simple linear regression is a basic regression model with only one predictor variable (X), and the regression function is linear. These models include, but are not limited to, simple linear, multiple linear, nonlinear, orthogonal, calibration, logistic, and Poisson. There are many different types of regression models. Regression analysis becomes a unique statistical tool for researchers, process engineers, and others in various fields. Prediction enables the researcher to answer “what if” questions, e.g., setting the independent variable (X) to a non-common value outside of the control range will likely produce what given output of the dependent variable (Y)? Many times, these three purposes overlap in practice. Control allows the researcher to set bounds on the independent variable (X) to achieve a controlled output range of the dependent variable (Y). Explanation describes the statistical relationship between the dependent variable (Y) and the independent variable (X). Regression analysis provides the researcher with three essential purposes: 1) explanation, 2) control, and 3) prediction. The expression of the general tendency of a dependent variable (Y) and an independent variable (X) is potent in many different fields. 414), implying that there are random errors present, hence the non-perfect fit. However, the approximate nature of the model must always be borne in mind” (p. Essentially, all models are wrong, but some are useful. Box (2007) states, “all models are approximations. The independent variable (X) is also referred to as the predictor variable. Ī regression model is a formal means of expressing the general tendency of a dependent variable (Y) to vary with the independent variable (X) systematically. It is commonly accepted that the term ‘regression’ describes the statistical, not the functional relationship between variables. For example, cholesterol levels and body weight have a non-perfect fit. Statistical relationships typically do not have perfect fits. For example, ice cream cones cost $1 each, so that one can buy 10 ice cream cones for $10 or 20 ice cream cones for $20.
Functional relationships have perfect fits. These relationships are either functional or statistical. Regression analysis utilizes the relationship between quantitative variables to predict one variable from one or more other variables. Keywords: nonlinear regression, statistical relationship, Solver, ENIG Linear and nonlinear regression methods are reviewed, and a worked example using electroless nickel immersion gold (ENIG) is provided.
Multiple nonlinear regression excel how to#
Understanding how to choose the proper model and starting parameters is critical. Nonlinear regression is a powerful statistical tool, but it can be challenging to find the appropriate model and starting parameters.


 0 kommentar(er)
0 kommentar(er)
